Dry Tank Technology, Technical Description

Since the Dry Tank Technology is primarily concerned with the removal of water from compressed air it is easiest to analyse the mechanisms which affect this process by considering the compressed air as a simplified gas mixture. Analysis of the dry compressed air to water vapour and liquid content at various positions within the compression process will enable us to compare the relative merits of this technology compared with a conventional air compression process. Since liquid water within any air compressor system can be easily measured and removed the quality of the compressed air and any further water vapour to liquid transformation is usually dictated by the water vapour concentration. One figure of merit which will aid in determining the total amount of water vapour present is the dew point temperature of the compressed air. The dew point temperature is a measure of how much water vapour is present within the gas. It provides a simple reference figure that can used to both quantitatively and qualitatively evaluated the amount of water present in a system.

This page provides a review of a number of physical principles relating to the evaluation of water in compressed air, details a number of useful formulae, provides calculated examples and useful tabulated data and external links to more comprehensive information.

Contents

Composition of the Air

Dry Air Supply Technical Description: Composition of air. — ©AGISEN Limited 2017

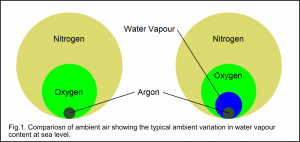
At sea level, and up to ~100 kms, the gas composition of ambient air is very consistent. By volume , dry air contains ~78% nitrogen, ~21% oxygen, 1% argon and 0.04% carbon dioxide and a tiny amount of other gases. In addition to the dry air component gases, ambient air also contains a variable amount of water vapour. Unlike the other main constituent of dry air the concentration of water vapour depends very much upon local weather and temperature conditions. Fig.1. indicates that the typical percentage variation of water vapour content is significant; typically overall changes in ambient air concentrations of between 0.001 and 5% are possible.

Partial Pressure

In a mixture of gases, each gas has a partial pressure which is the hypothetical pressure of that gas if it alone occupied the entire volume of the original mixture at the same temperature. Therefore the total pressure of an ideal gas mixture is the sum of the partial pressure of each gas in the mixture. Whilst ambient air is a multi-component gas mixture the volumetric stability of the dry gas mixture allows us to consider, in these examples, all the dry gas constituent as a single gas. The compressed ambient air can therefore be considered as a simple two component (dry gases and water vapour) mixture. This simplifies the following calculations quite a bit.

Pressure units

The modern unit of pressure measurement is the pascal (Pa) and like all units of pressure represents a force applied over a defined area. In this case:

(1) $\begin{equation*}\mathrm{1\ Pa = 1 \dfrac{N}{m^{2}}=1 \dfrac{kg}{ms^{2}}}\end{equation*}$

For conversion purposes:

(2) $\begin{equation*}\mathrm{1\ bar = 10^{5}\ Pa = 100,000\ Pa = 100\ kPa = 1000\ hPa}\end{equation*}$

and standard atmospheric pressure (atm) is given as:

(3) $\begin{equation*}\mathrm{1\ atm\ = 101,325\ Pa\ \mathrm{or}\ 1013.25\ hPa}\end{equation*}$

For the purposes of this page we will stick with $\mathrm{hPa}$ unit.

Dalton’s Law

Dalton’s Law of partial pressures states that in a mixture of non-reacting gases, the total pressure is equal to the sum of the partial pressures of the component gases within the mixture.

(4) $\begin{equation*} p_{total}=\sum_{i=1}^{n}p_{i} \end{equation*}$

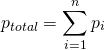
(5) $\begin{equation*} p_{total}=p_{1}+p_{2}+p_{3}+...+p_{n} \end{equation*}$

where $p_{1}, p_{2},...,p_{n}$ represents the partial pressures of each component gas. For example when we look at air we have:

(6) $\begin{equation*}p_{total}=p_{N_{2}}+p_{O_{2}}+p_{Ar}+...+p_{H_{2}O}\end{equation*}$

which we will simply to:

(7) $\begin{equation*}p_{total}=p_{dry}+p_{H_{2}O}\end{equation*}$

Vapour pressure and Relative humidity

Vapour pressure is defined as the pressure exerted by a vapour in thermodynamic equilibrium with its condensed phases (liquid or solid) at a given temperature in a closed system. In other words, if you place some water in a container e.g. a water bottle and seal the top then some of the water will evaporate and form a vapour above the liquid water. At some point, depending on the temperature of the room (or your hand) the rate of water evaporation and the rate of condensation (vapour back into liquid) will be the same. The pressure exerted by the vapour above the water is known as the vapour or saturated vapour pressure as in this case the air above the water contains the maximum amount of water it will support.

If at atmospheric pressure the air is completely saturated with water then the air has a relative humidity of 100%. However, in most locations and at most times the air is not fully saturated and has a relative humidity of somewhat less than 100%. The relative humidity, at all temperatures, is defined as:

(8) $\begin{equation*}\mathrm{RH = \dfrac{P_{w}}{P_{ws}}\times 100\%}\end{equation*}$

where $P_{w}$ is the partial pressure of the water in the air and $P_{ws}$ is the saturated partial pressure of the water in air, the equation for which is given below.

Water vapour saturation pressure

(9) $\begin{equation*} \vartheta=1-\dfrac{T}{T{c}} \end{equation*}$

(10) $\begin{equation*} \ln\left( \dfrac{P{ws}}{P{c}}\right)=\dfrac{T{c}}{T}\left[C_{1}\vartheta+C_{2}\vartheta^{1.5}+C_{3}\vartheta^{3}+C_{4}\vartheta^{3.5}+C_{5}\vartheta^{4}+C_{6}\vartheta^{7.5} \right] \end{equation*}$

where
$T$ = Temperature in K, $P_{ws}$ = Saturation vapour pressure (hPa), $T_{c}$ = Critical temperature, 647.096K, $P_{c}$ = Critical pressure, 220,640 hPa
and the $C_{1}$ to $C_{6}$ constants are given as: $C_{1}$ = -7.85951783, $C_{2}$ = 1.84408259, $C_{3}$ = -11.7866497, $C_{4}$ = 22.6807411, $C_{5}$ = -15.9618719 and $C_{6}$ = 1.80122502.

(11) $\begin{equation*}P_{ws} = P_{c}\ exp\left[\dfrac{T_{c}}{T}\left( C_{1}\vartheta+C_{2}\vartheta^{1.5}+C_{3}\vartheta^{3}+C_{4}\vartheta^{3.5}+C_{5}\vartheta^{4}+C_{6}\vartheta^{7.5}\right) \right] \end{equation*}$

As an example, using the equations above the saturation pressure of water in air $P_{ws}$ at $25^{\circ}C$ is $31.7\ hPa$ and the partial pressure of the water vapour $P_{w}$ in 70% RH air is just 70% of this figure or $22.19\ hPa$ .

By using these simple, albeit long winded, calculations we now have a method of obtaining the partial pressure water vapour in ambient air and, as subsequent sections will show, a simple method of tracing the water content, whether water or vapour, through the compression process.

Calculation of dew point from RH

The dew point of the air can be also be calculated using the partial pressure of the air obtained from the equations in the section above. Using the partial pressure value $P_{w}$ for the water in air of a known humidity we can use the following equation to obtain the dew point of the air.

(12) $\begin{equation*}T_{d} = \dfrac{T_{n}}{\left[ \dfrac{m}{log_{10}\left( \dfrac{P_{w}}{A}\right)}-1\right] }\end{equation*}$

where the constants $T_{n}$ , $m$ and $A$ can be taken from the table:

Dry Air Supply Technical Description: Table of equation constants. — ©AGISEN Limited 2017

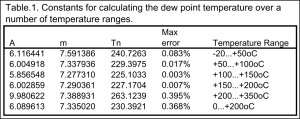
Using the previous example for $70\%$ RH air at $25^{\circ}C$ which has a water partial pressure $P_{w}$ of $22.19\ hPa$ in this equation (using the first line of constants) gives a dew point temperature of $19.16^{\circ}C$ . This tells us that if ambient air, with this temperature and humidity, is in contact with a cold surface at a temperature below ~ $19^{\circ}c$ that the water in the air will condense and liquid water will be formed; identical to the situation in which water forms on the outer surface of a cold can of coke on a summers day.

As the air/water vapour mixture is compressed then the partial pressure of the water vapour within the mixture is also compressed.

(13) $\begin{equation*}P_{w_{pres}} = \dfrac{P_{pres}}{P_{amb}} \cdot P_{w}\end{equation*}$

where $P_{w_{pres}}$ is the partial pressure of the water in the compressed air, $P_{w}$ is the partial pressure of the water at ambient pressure (usually $1013.25\ hPa$ ), $P_{pres}$ is the elevated pressure condition and $P_{amb}$ is the ambient pressure.\\

So, taking the sample of the previous air when it is compressed to $8\ \mathrm{bar(g)}$ or $9000\ hPa$ (note absolute pressure is used in these equations) then the partial pressure of the water is raised from $22.19\ hPa$ to $197.1\ hPa$ . Now lets look at what affect this has on the dew point of the compressed air or its pressure dew point.

Pressure dew point (PDP)

The term pressure dew point is used when referring to the dew point temperature of a gas (containing water vapour) at an elevated pressure, above atmospheric. Since this is as good as the definition gets it’s extremely important that the actual pressure is known in order to place the dew point figure in some context.

(14) $\begin{equation*}T_{d_{pres}} = \dfrac{T_{n}}{\left[ \dfrac{m}{log_{10}\left( \dfrac{P_{w_{pres}}}{A}\right)}-1\right] }\end{equation*}$

Graph show the pressure above which liquid water id formed for various ambient relative humidity values. — © AGISEN Limited 2017

Using the previous figure for the partial pressure at elevated pressure we obtain a dew point temperature for the compressed air of $59.68^{\circ}C$ . So at any temperature below this figure, for example the inside of the main receiver, the water vapour will condense and there will be both water vapour and liquid water in the compressed air system.

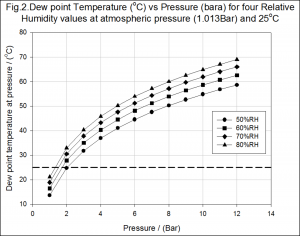
We have seen that as a volume of air is compressed that the partial pressure of the water vapour and the dew point temperature of the gas both increase. This shouldn’t be a shock as we all know that when air is compressed water is produced within the receiver and system pipework. However, it may be of a little more interest to look at how little compression is needed to induce water generation, Fig2.

The pressure values along the abscissa are absolute pressure readings. These plots indicate that even a small amount of compression , $1\ \mathrm{bar(g)}$ , is capable of producing compressed gas with a dew point temperature above ambient. Therefore, even in the driest of areas, it is almost certain that water will be present within a compressed air system.

Absolute humidity (what type of water do I have!)

The above equations have given us an idea about when, at what temperature, the water vapour in the compressed air will start to turn into liquid water within the compressor system. However, in order to get a more quantitative indication we need to know how much of this ambient moisture is in the form of water and how much is in the vapour phase. We can get a good idea about this by obtaining a figure for the absolute humidity of the air at various points in the system. We can accomplish this by obtaining the saturated partial pressures at known temperature points in the system, working out what the partial pressure returns to at ambient pressure and again calculating the absolute humidity. We now have a figure for absolute humidity of the air before entering the system and when it exits: the difference is the amount of water generated and in the system. A simple equation for the absolute humidity is given as:

(15) $\begin{equation*}H_{abs}=C\cdot\dfrac{P_{w}}{T}\end{equation*}$

where $C = 2.16679\ gKJ^{-1}$ , $P_{w}$ is the vapour pressure in $Pa$ and $T$ the temperature in Kelvin. Whereas the saturated vapour pressure at a temperature T is given by the equation:

(16) $\begin{equation*}P_{ws}=P_{c}\exp\left[\dfrac{T_{c}}{T}\left(C_{1}\vartheta+C_{2}\vartheta^{1.5}+C_{3}\vartheta^{3}+C_{4}\vartheta^{3.5}+C_{5}\vartheta^{4}+C_{6}\vartheta^{7.5} \right) \right]\end{equation*}$

or more simply as:

(17) $\begin{equation*}P_{ws}=A{\cdot} 10^{\left( \dfrac{mT}{T+T_{n}} \right) }\end{equation*}$

where $A$ , $m$ and $T_{n}$ are the previous constants used and $T$ is the temperature $\left(^{\circ}C \right)$ .

Carrying on from the previous example. If the receiver is at a temperature of then the saturated partial pressure for water at this temperature is $\sim31.7\ hPa$ . When returned to ambient pressure the vapour pressure of the water vapour will be reduced to $3.6\ hPa$ and, using the first equation in this section above, will have an absolute humidity of $\sim2.6\ gm^{-3}$ . Since the partial pressure of the water vapour in ambient air, prior to compression, was $15.85\ hPa$ and the absolute humidity was $11.52\ gm^{-3}$ then $\sim77.5\%$ of the water that was in the ambient air is now in the form of liquid water within the system. The remainder of the water is still in the vapour phase.

References

Atlas Copco Airpower NV, 2015. Atlas Copco Compressed Air Manual, 8^th Edition. [pdf] Belgium. Available at: http://www.atlascopco.com/Images/Compressed_Air_Manual_tcm30-1249312.pdf

Dew Point in Compressed Air – Frequently Asked Questions, Vaisala Application Note, 2013. http://www.vaisala.com/Vaisala%20Documents/Application%20notes/Dew-point-compressed-air-Application-note-B210991EN-B-LOW-v1.pdf

Humidity Conversion Formulas, Calculations formulas for Humidity, Vaisala 2013. http://www.vaisala.com/Vaisala%20Documents/Application%20notes/Humidity_Conversion_Formulas_B210973EN-F.pdf

Air Compressor, Selection & Application, 1/4 through 30HP, CAGI, 2016, http://www.cagi.org/pdfs/CAGIAirCompressorHP.pdf

Wagner, W. and Pruß, A., The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. Journal of Physical and Chemical Reference Data, June 2002, Vol. 31, Issue 2, pp387535 [pdf], http://thermophysics.ru/pdf_doc/IAPWS_1995.pdf [accessed 2017]